Common Lisp the Language, 2nd Edition




Next: Examples
Up: Determining the Class
Previous: Determining the Class

Topological sorting proceeds by finding a class C in 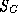 such
that no other class precedes that element according to the elements
in R. The class C is placed first in the result.
Remove C from
such
that no other class precedes that element according to the elements
in R. The class C is placed first in the result.
Remove C from 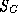 , and remove all pairs of the form
(C, D),
, and remove all pairs of the form
(C, D),
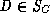 , from R. Repeat the process, adding
classes with no predecessors to the end of the result. Stop when no
element can be found that has no predecessor.
, from R. Repeat the process, adding
classes with no predecessors to the end of the result. Stop when no
element can be found that has no predecessor.
If 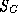 is not empty and the process has stopped, the set R is
inconsistent. If every class in the finite set of classes is preceded
by another, then R contains a loop. That is, there is a chain of
classes
is not empty and the process has stopped, the set R is
inconsistent. If every class in the finite set of classes is preceded
by another, then R contains a loop. That is, there is a chain of
classes 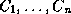 such that
such that 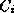 precedes
precedes
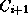 , 1 <= i < n,
and
, 1 <= i < n,
and 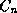 precedes
precedes 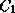 .
.
Sometimes there are several classes from 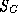 with no
predecessors. In this case select the one that has a direct
subclass rightmost in the class precedence list computed so far.
with no
predecessors. In this case select the one that has a direct
subclass rightmost in the class precedence list computed so far.
If there is no
such candidate class, R does not generate a partial ordering - the
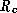 ,
, 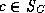 , are inconsistent.
, are inconsistent.
In more precise terms, let 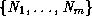 ,
m >= 2, be
the classes from
,
m >= 2, be
the classes from 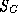 with no predecessors. Let
with no predecessors. Let 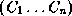 , n >= 1, be the class precedence list
constructed so far.
, n >= 1, be the class precedence list
constructed so far. 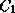 is the most specific class, and
is the most specific class, and 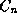 is the least specific. Let 1 <= j <= n be the largest number
such that there exists an i where 1 <= i <= m and
is the least specific. Let 1 <= j <= n be the largest number
such that there exists an i where 1 <= i <= m and
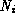 is a direct superclass of
is a direct superclass of 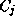 ;
;
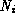 is placed next.
is placed next.
The effect of this rule for selecting from a set of classes with no
predecessors is that classes in a simple superclass chain are
adjacent in the class precedence list and that classes in each
relatively separated subgraph are adjacent in the class
precedence list. For example, let 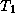 and
and 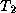 be subgraphs
whose only element in common is the class J. Suppose
that no superclass of J appears in either
be subgraphs
whose only element in common is the class J. Suppose
that no superclass of J appears in either 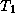 or
or 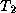 .
Let
.
Let 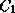 be the bottom of
be the bottom of 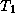 ; and let
; and let 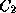 be the
bottom of
be the
bottom of 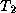 . Suppose C is a class whose direct superclasses
are
. Suppose C is a class whose direct superclasses
are 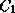 and
and 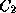 in that order; then the class precedence
list for C will start with C and will be followed by all classes
in
in that order; then the class precedence
list for C will start with C and will be followed by all classes
in 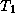 except J. All the classes of
except J. All the classes of 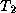 will be next.
The class J and its superclasses will appear last.
will be next.
The class J and its superclasses will appear last.





Next: Examples
Up: Determining the Class
Previous: Determining the Class
AI.Repository@cs.cmu.edu

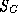 such
that no other class precedes that element according to the elements
in R. The class C is placed first in the result.
Remove C from
such
that no other class precedes that element according to the elements
in R. The class C is placed first in the result.
Remove C from 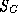 , and remove all pairs of the form
(C, D),
, and remove all pairs of the form
(C, D),
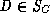 , from R. Repeat the process, adding
classes with no predecessors to the end of the result. Stop when no
element can be found that has no predecessor.
, from R. Repeat the process, adding
classes with no predecessors to the end of the result. Stop when no
element can be found that has no predecessor.
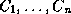 such that
such that 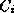 precedes
precedes
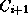 , 1 <= i < n,
and
, 1 <= i < n,
and 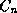 precedes
precedes 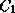 .
.
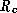 ,
, 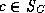 , are inconsistent.
, are inconsistent.
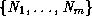 ,
m >= 2, be
the classes from
,
m >= 2, be
the classes from 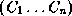 , n >= 1, be the class precedence list
constructed so far.
, n >= 1, be the class precedence list
constructed so far. 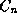 is the least specific. Let 1 <= j <= n be the largest number
such that there exists an i where 1 <= i <= m and
is the least specific. Let 1 <= j <= n be the largest number
such that there exists an i where 1 <= i <= m and
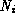 is a direct superclass of
is a direct superclass of 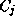 ;
;
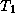 and
and 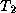 be subgraphs
whose only element in common is the class J. Suppose
that no superclass of J appears in either
be subgraphs
whose only element in common is the class J. Suppose
that no superclass of J appears in either 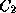 be the
bottom of
be the
bottom of 