Common Lisp the Language, 2nd Edition




Next: Complex Numbers
Up: Numbers
Previous: Ratios
Common Lisp allows an implementation to provide one or more kinds of
floating-point number, which collectively make up the type float.
Now a floating-point number is a (mathematical)
rational number of the form
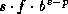 ,
where s is +1 or -1, the sign;
b is an integer greater than 1,
the base or radix of the representation;
p is a positive integer,
the precision (in base-b digits) of the floating-point number;
f is a positive integer between
,
where s is +1 or -1, the sign;
b is an integer greater than 1,
the base or radix of the representation;
p is a positive integer,
the precision (in base-b digits) of the floating-point number;
f is a positive integer between
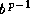 and
and 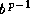 (inclusive),
the significand;
and e is an integer, the exponent.
The value of p and the range of e
depends on the implementation and on the type of floating-point number
within that implementation.
In addition, there is a floating-point zero;
depending on the implementation, there may also be a ``minus zero.''
If there is no minus zero, then 0.0 and -0.0 are
both interpreted as simply a floating-point zero.
(inclusive),
the significand;
and e is an integer, the exponent.
The value of p and the range of e
depends on the implementation and on the type of floating-point number
within that implementation.
In addition, there is a floating-point zero;
depending on the implementation, there may also be a ``minus zero.''
If there is no minus zero, then 0.0 and -0.0 are
both interpreted as simply a floating-point zero.
Implementation note: The form of the above description should not be construed
to require the internal representation to be in sign-magnitude form.
Two's-complement and other representations are also acceptable. Note
that the radix of the internal representation may be other than 2, as on
the IBM 360 and 370, which use radix 16; see
float-radix.
Floating-point numbers may be provided in a variety of precisions and sizes,
depending on the implementation. High-quality floating-point
software tends to depend critically on the precise nature of the
floating-point arithmetic and so may not always be completely portable.
As an aid in writing programs that are
moderately portable, however, certain definitions are made here:
-
A short floating-point number (type short-float)
is of the representation of smallest
fixed precision provided by an implementation.
-
A long floating-point number (type long-float)
is of the representation of the largest fixed
precision provided by an implementation.
-
Intermediate between short and long formats are two others, arbitrarily
called single and double (types single-float and double-float).
The precise definition of these categories is implementation-dependent.
However, the rough intent is that short floating-point numbers be
precise to at least four decimal places (but also have
a space-efficient representation);
single floating-point numbers, to at least seven decimal places;
and double floating-point numbers, to at least fourteen decimal places.
It is suggested that
the precision (measured in bits, computed as 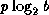 )
and the exponent size (also measured in bits, computed as the base-2
logarithm of 1 plus the maximum exponent value) be at least as great
as the values in table 2-1.
)
and the exponent size (also measured in bits, computed as the base-2
logarithm of 1 plus the maximum exponent value) be at least as great
as the values in table 2-1.

Floating-point numbers are written in either decimal fraction
or computerized scientific notation: an optional sign,
then a non-empty sequence of digits with an embedded decimal point,
then an optional decimal exponent specification.
If there is no exponent specifier, then
the decimal point is required, and there must be digits
after it.
The exponent specifier consists of an exponent marker,
an optional sign, and a non-empty sequence of digits.
For preciseness, here is a modified-BNF description of floating-point
notation.
floating-point-number ::= [sign] {digit}* decimal-point {digit}* [exponent]
| [sign] {digit}+ [decimal-point {digit}*] exponent
sign ::= + | -
decimal-point ::= .
digit ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
exponent ::= exponent-marker [sign] {digit}+
exponent-marker ::= e | s | f | d | l | E | S | F | D | L
If no exponent specifier is present, or if the exponent marker e
(or E) is used, then the precise format to be used is not
specified. When such a representation is read and
converted to an internal floating-point data object, the format specified
by the variable *read-default-float-format* is used; the initial
value of this variable is single-float.
The letters s, f, d, and l (or their
respective uppercase equivalents) explicitly specify the
use of short, single, double, and long format, respectively.
Examples of floating-point numbers:
0.0 ;Floating-point zero in default format
0E0 ;Also floating-point zero in default format
-.0 ;This may be a zero or a minus zero,
; depending on the implementation
0. ;The integer zero, not a floating-point zero!
0.0s0 ;A floating-point zero in short format
0s0 ;Also a floating-point zero in short format
3.1415926535897932384d0 ;A double-format approximation to  6.02E+23 ;Avogadro's number, in default format
602E+21 ;Also Avogadro's number, in default format
3.010299957f-1 ;
6.02E+23 ;Avogadro's number, in default format
602E+21 ;Also Avogadro's number, in default format
3.010299957f-1 ;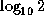 , in single format
-0.000000001s9 ;
, in single format
-0.000000001s9 ; in short format, the hard way
in short format, the hard way

Notice of correction.
The first edition unfortunately listed an incorrect value (3.1010299957f-1)
for the base-10 logarithm of 2.

The internal format used for an external representation depends only
on the exponent marker and not on the number of decimal digits
in the external representation.
While Common Lisp provides terminology and notation sufficient
to accommodate four distinct floating-point formats,
not all implementations will have the means to support
that many distinct formats.
An implementation is therefore permitted to provide
fewer than four distinct internal floating-point formats,
in which case at least one of them will be ``shared''
by more than one of the external format names short, single,
double, and long according to the following rules:
-
If one internal format is provided, then it is considered to be
single, but serves also as short, double, and long.
The data types short-float,
single-float, double-float, and long-float are
considered to be identical. An expression such as (eql 1.0s0 1.0d0)
will be true in such an implementation
because the two numbers 1.0s0 and 1.0d0 will
be converted into the same internal format and therefore be considered
to have the same data type, despite the differing external syntax.
Similarly, (typep 1.0L0 'short-float) will be true in such
an implementation.
For output purposes all floating-point numbers are assumed to be
of single format and thus will print using the
exponent letter E or F.
-
If two internal formats are provided, then either of two correspondences
may be used, depending on which is the more appropriate:
-
One format is short; the other is single and serves also
as double and long.
The data types
single-float, double-float, and long-float are
considered to be identical, but short-float is distinct.
An expression such as (eql 1.0s0 1.0d0)
will be false, but (eql 1.0f0 1.0d0) will be true.
Similarly, (typep 1.0L0 'short-float) will be false,
but (typep 1.0L0 'single-float) will be true.
For output purposes all floating-point numbers are assumed to be
of short or single format.
-
One format is single and serves also as short;
the other is double and serves also as long.
The data types short-float and single-float are considered to be
identical, and the data types double-float and long-float are
considered to be identical.
An expression such as (eql 1.0s0 1.0d0)
will be false, as will (eql 1.0f0 1.0d0);
but (eql 1.0d0 1.0L0) will be true.
Similarly, (typep 1.0L0 'short-float) will be false,
but (typep 1.0L0 'double-float) will be true.
For output purposes all floating-point numbers are assumed to be
of single or double format.
-
If three internal formats are provided, then either of two correspondences
may be used, depending on which is the more appropriate:
-
One format is short; another format is single; and the third format is
double and serves also as long. Similar constraints apply.
-
One format is single and serves also as short;
another is double; and the third format is long.
Implementation note: It is recommended that an implementation
provide as many distinct floating-point formats as feasible,
using table 2-1 as a guideline.
Ideally, short-format floating-point numbers should have an
``immediate'' representation that does not require heap allocation;
single-format
floating-point numbers should approximate IEEE proposed standard
single-format floating-point numbers; and double-format floating-point
numbers should approximate IEEE proposed standard double-format
floating-point numbers
[23,17,16].




Next: Complex Numbers
Up: Numbers
Previous: Ratios
AI.Repository@cs.cmu.edu
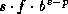 ,
where s is +1 or -1, the sign;
b is an integer greater than 1,
the base or radix of the representation;
p is a positive integer,
the precision (in base-b digits) of the floating-point number;
f is a positive integer between
,
where s is +1 or -1, the sign;
b is an integer greater than 1,
the base or radix of the representation;
p is a positive integer,
the precision (in base-b digits) of the floating-point number;
f is a positive integer between
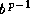 and
and 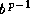 (inclusive),
the significand;
and e is an integer, the exponent.
The value of p and the range of e
depends on the implementation and on the type of floating-point number
within that implementation.
In addition, there is a floating-point zero;
depending on the implementation, there may also be a ``minus zero.''
If there is no minus zero, then 0.0 and -0.0 are
both interpreted as simply a floating-point zero.
(inclusive),
the significand;
and e is an integer, the exponent.
The value of p and the range of e
depends on the implementation and on the type of floating-point number
within that implementation.
In addition, there is a floating-point zero;
depending on the implementation, there may also be a ``minus zero.''
If there is no minus zero, then 0.0 and -0.0 are
both interpreted as simply a floating-point zero.
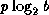 )
and the exponent size (also measured in bits, computed as the base-2
logarithm of 1 plus the maximum exponent value) be at least as great
as the values in table 2-1.
)
and the exponent size (also measured in bits, computed as the base-2
logarithm of 1 plus the maximum exponent value) be at least as great
as the values in table 2-1.

 6.02E+23 ;Avogadro's number, in default format
602E+21 ;Also Avogadro's number, in default format
3.010299957f-1 ;
6.02E+23 ;Avogadro's number, in default format
602E+21 ;Also Avogadro's number, in default format
3.010299957f-1 ;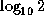 , in single format
-0.000000001s9 ;
, in single format
-0.000000001s9 ; in short format, the hard way
in short format, the hard way

